I use simple definition of legality: 1. Side to move does not give check. (2. No pawns on promotion rank or before the starting rank. 3. Exactly one white king and exactly one black king are on the board). Often people define legal position as the one that can be obtained from the starting position after a sequence of legal moves. I don't use this for practical reasons: 1. Verifying the relation to the starting position can be non-trivial and time consuming. 2. In some chess variants there is no established starting position.
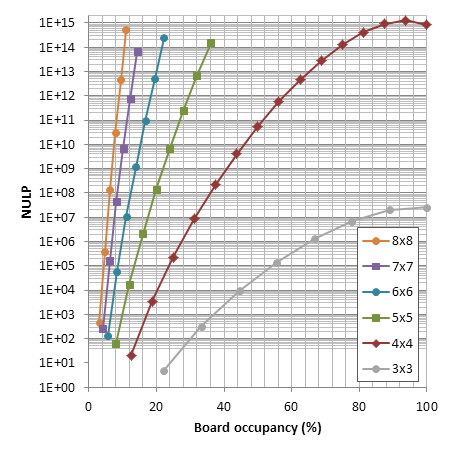
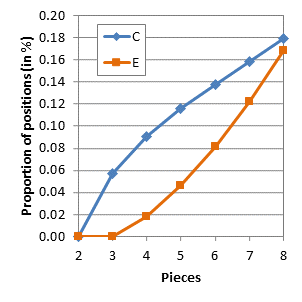
The uniqueness concept is similarly simple: The number of unique legal positions should count only one position out of all of its symmetrical equivalent variants. This includes swapping the side to move, and also diagonal symmetries and rotations of the board. An example can be seen on 4x4 chess site.
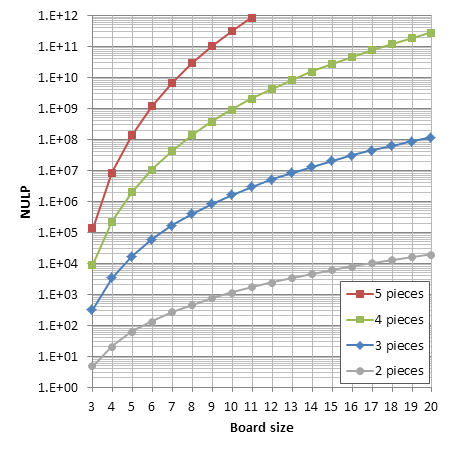
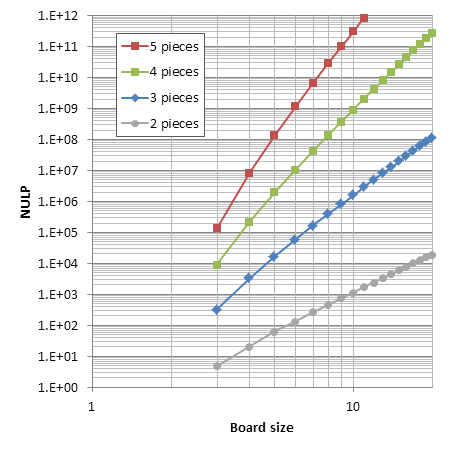
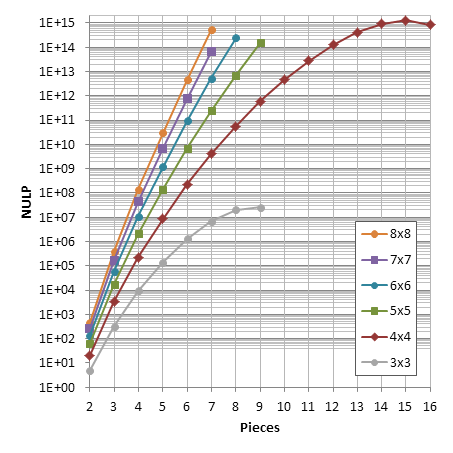
Although chess endgame have been studied to great depth, I've been unable to find the numbers of unique legal positions in chess endgames. If someone knows of any reports of such numbers, I'll appreciate if you direct me to them.
The number of 2-piece positions (bare kings) in chess is well known: 462. However, not for 3 pieces or more (AFAIK). Last year Guy Haworth kindly posted statistics from Nalimov tablebases up to 6 pieces. These numbers are a good start, except for these issues: 1. Some positions are counted twice (diagonally symmetrical positions with kings on the main diagonal, as far as I understand). 2. Positions with castling rights are not counted. 3. 5-vs-1 positions are not counted.
My current numbers for chess are:
Thanks,
Kirill
 . . .
. . . 
 . . .
. . .