4x4 Chess
Unique Legal Positions
The number of unique legal positions (NULP) is a basic measure of game state-space complexity. The defining features of this number: 1. Only legal positions are counted. 2. Only unique positions are counted. Please check the NULP web-site for detailed discussion.
Some definitions:
Position - Any placement of pieces on a 4x4 board (one piece per square, so from 0 to 16 pieces can be present), plus information about what side has the right to move (either white or black).
Legal position - Any position that has one white and one black king, where side to move does not give a check (does not attack opponent's king), and where there are no white pawns on 4-th rank and no black pawns on 1-st rank.
Unique position - In the context of counting positions, number of unique positions means that we count all symmetrical variants of one position as single position. All possible symmetries are considered, including horizontal, vertical, diagonal or any combination (which effectively includes board rotation as well). Also this includes changing the side to move and swapping the piece colors. Example - all of the following positions are counted as just one position for the NULP:
In this case 16 different positions in fact correspond to just one unique position. In other cases proportion of unique positions may differ from 1/16, particularly when pawns are included, or when position is diagonally symmetrical.
Game or Puzzle?
A game should have a starting position. 4x4 chess does not have one, so technically it's not even a game, but perhaps some sort of puzzle. A puzzle can have many possible initial positions, and some goal should be reached through a sequence of legal moves. This is exactly what 4x4 chess is in the current form. All possible initial positions are allowed, and the goal is to checkmate against the best defense (or against any defense).
In a game (like 8x8 chess) legal positions are those that can be reached from the starting position with a sequence of legal moves. This strict definition makes for a very narrow set of legal positions. In a puzzle setting (like 4x4 chess), on the other hand, any position can be the initial one, creating a much larger and more interesting set of positions.
Most games can be generalized into puzzles by discarding the starting position and instead looking at all possible positions that don't directly break the other rules. Strong solution of such puzzle may be harder to obtain, but also provides more information and more fun. For example, it may allow to find alternative interesting starting positions. Such "ultra-strong" solution was obtained for 3x4 chess in 2009, and is what I am aiming for in 4x4 chess.
4x4 chess NULP
The total number of unique legal position in 4x4 chess is 3,677,542,994,054,890. About 3.68 quadrillions, or about 3.68 peta-positions. A 16-digit (52-bit) number.
This number was obtained by meticulously counting all possible unique legal positions, using idle mode of the solver (where it just counts the positions without solving them). This task itself already took some weeks (faster counting is possible, but was not a priority).
Of course, independent verification would be more than welcome!
Comparing 4x4 chess with other games and puzzles:
| Game/Puzzle | State-space complexity | Source |
| 3x3 Chess, all unique legal positions (no starting position) | 5.5 x 107 | sashawww, 2011 |
| 6x6 Othello (Reversi), all reachable from standard starting position | 4.0 x 1010 | Feinstein, 1993 |
| 3x4 Chess, all unique legal positions (no starting position) | 1.7 x 1011 | Kryukov, 2009 |
| 5x5 Go | 4.1 x 1011 | Tromp, 2005 |
| Connect Four (standard 7x6 board) | 4.5 x 1012 | Tromp, 2010 |
| 4x4 Chess, all unique legal positions (no starting position) | 3.7 x 1015 | |
| 6x6 Go | 6.3 x 1016 | Tromp, 2005 |
| Rubik's cube, all positions that can be solved without disassembling the cube | 4.3 x 1019 | Rokicki, Kociemba and Davidson, 2010 |
| English Draughts (Checkers), all reachable from starting position | 5.0 x 1020 | Schaeffer et al., 2007 |
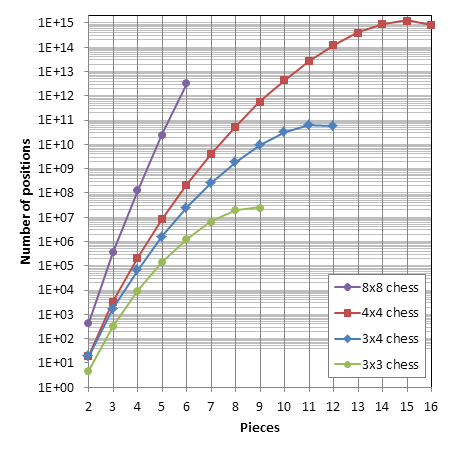
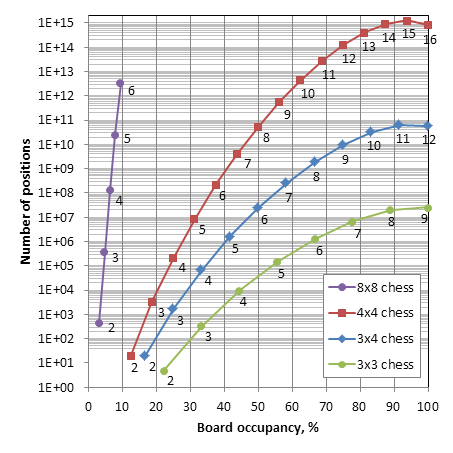
In particular, 4x4 chess is 21,981 times larger than 3x4 chess and 67,075,421 times larger than 3x3 chess.
If you spend 1 millisecond thinking about each 4x4 chess position, it will take about 117 thousand years to visit all of them.
If you use 1 byte to store each position, you'll need 3.68 petabytes, which means 1226 hard disks of 3 TB each. If you only use 1 bit per position, you still need 460 terabytes, or 153 x 3 TB hard disks. (Fortunately, even better compression is possible).
(Also 3,677,542,994,054,890 factorizes into 2 x 5 x 367,754,299,405,489).
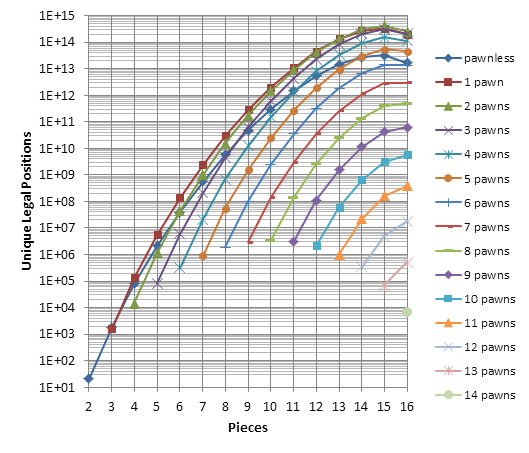
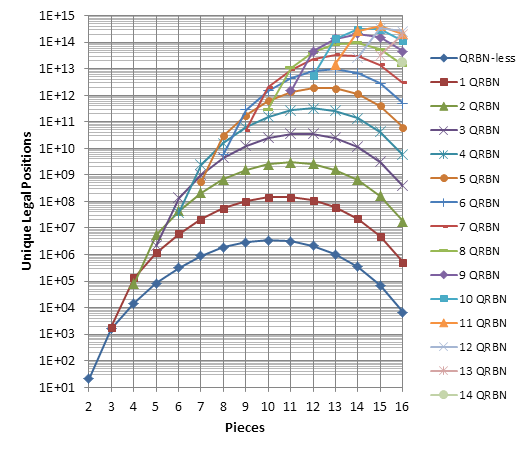
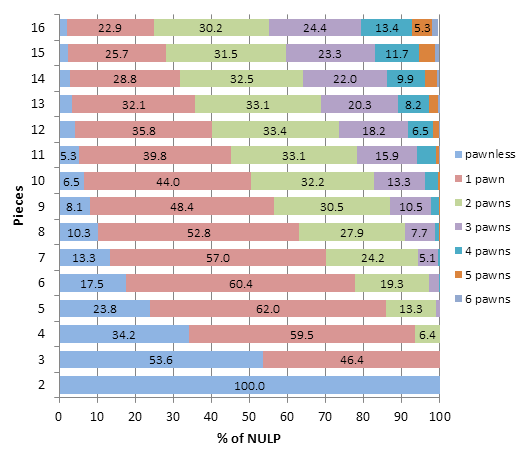
NULP by number of pieces
| Pieces | Unique legal positions |
| 2 | 21 |
| 3 | 3,378 |
| 4 | 227,362 |
| 5 | 8,803,638 |
| 6 | 226,104,696 |
| 7 | 4,143,416,867 |
| 8 | 56,389,004,075 |
| 9 | 582,127,548,496 |
| 10 | 4,595,929,598,727 |
| 11 | 27,669,037,598,574 |
| 12 | 125,170,155,996,618 |
| 13 | 412,768,680,606,528 |
| 14 | 937,881,313,683,098 |
| 15 | 1,313,680,529,830,650 |
| 16 | 855,134,451,632,160 |
The plots below shows how NULP depends on adding extra pieces in 4x4 chess, compared to other board sizes.