No, not from me anyway. I won't even think about it until 4x4 is done, which will be probably years from now.ernest wrote:This is why I am quite interested by the "simpler" variant of 5x5 chess ("italian chess"):
kqbnr/ppppp/5/PPPPP/KQBNR
Any news about that?
4x4 chess
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
Re: 4x4 chess
I was thinking more of an extension of your computation order:
If you only allow say, knights and bishops, the database should fit on a single hard disk of today.
I realize I made some mistakes, but the idea should still hold. (To compute positions without few piece types, then add piece types as you can afford the computation and finally allowing pawns.)Kirill Kryukov wrote: b) pawnless endings -> all with 1 pawn -> all with 2 pawns -> ... -> all with 14 pawns
If you only allow say, knights and bishops, the database should fit on a single hard disk of today.
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Sure, for pawnless tables it will work very well.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
10-piece test run:
Index space: 5,612,237,340,802 positions
Unique legal: 4,601,321,236,958 positions (81.99% of index space)
Checkmates: 904,468,955,232 (19.66% of unique legal)
Comparing with 3x4 chess:
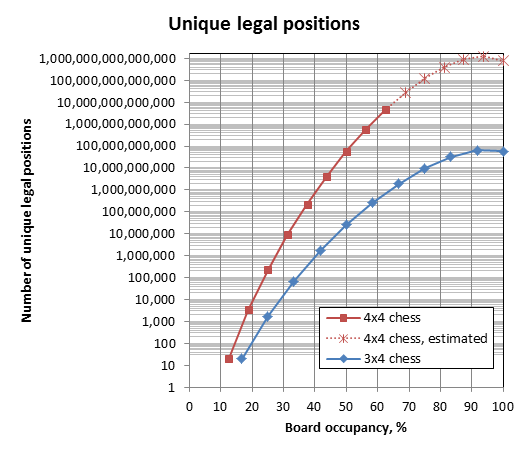
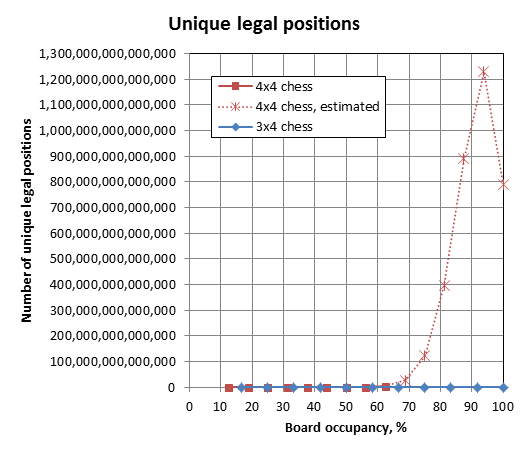
Estimated numbers are obtained by extrapolating the "upper bound / unique legal positions" ratio up to 16 pieces (using the data for 4-to-10 pieces), then applying this ratio to compute the estimation. The number is so large that it bugged my Excel to not show some of the grid lines.
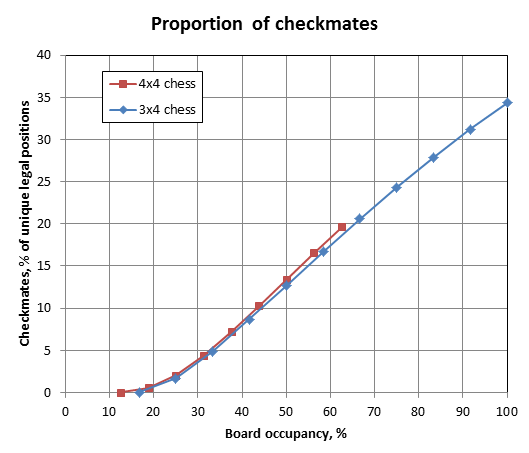
Nothing unexpected here. The gap from 3x4 is slowly increasing.
EDIT: Last edited on 2011-01-28 to update the graphs.
Index space: 5,612,237,340,802 positions
Unique legal: 4,601,321,236,958 positions (81.99% of index space)
Checkmates: 904,468,955,232 (19.66% of unique legal)
Comparing with 3x4 chess:


Estimated numbers are obtained by extrapolating the "upper bound / unique legal positions" ratio up to 16 pieces (using the data for 4-to-10 pieces), then applying this ratio to compute the estimation. The number is so large that it bugged my Excel to not show some of the grid lines.

Nothing unexpected here. The gap from 3x4 is slowly increasing.
EDIT: Last edited on 2011-01-28 to update the graphs.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
No other news, so I'll talk more about estimating the number of unique legal positions (NULP). In previous rough estimate I used the number of unique legal positions from 3x4, and the naively computed upper bound in both 3x4 and 4x4, under the assumption that the ratio in 4x4 is the same like in 3x4. Here I'll further refine that estimate.
This time we know the NULP for 2-to-10 pieces in 4x4, so we can use it for computing the overall estimate. First, let's look at 3x4 chess again. We know the NULP for each number of pieces on board (2 to 12). Let's compare it with the respective upper bound values, which is computed for N pieces as UB(N) = 40 * 10^(N-2) * C(10,N-2) (40 is the number of king placements):
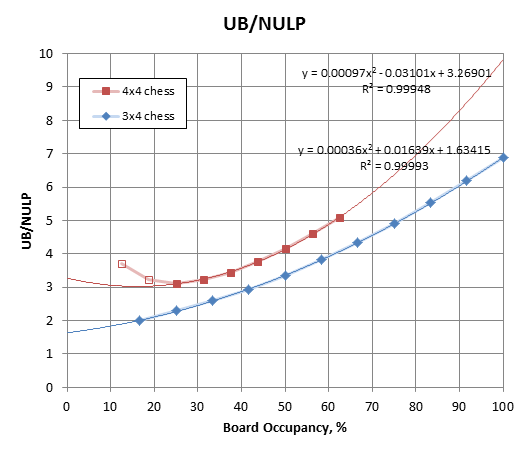
First thing that is apparent is that contraty to my previous simple assumption, the UB/NULP ratio is not the same between 3x4 and 4x4. It is consistently larger in 4x4, even if not much, and the gap is widening when larger part of the board is occupied.
Quadratic curve gives quite decent fit (4 to 10 pieces), so I extrapolated to 16 pieces, getting these ratios:
The estimated NULP (number of unique legal positions) in 4x4 chess is 20,680 times larger than the actual NULP in 3x4 chess.
EDIT: 2011-01-31: cleanup.
This time we know the NULP for 2-to-10 pieces in 4x4, so we can use it for computing the overall estimate. First, let's look at 3x4 chess again. We know the NULP for each number of pieces on board (2 to 12). Let's compare it with the respective upper bound values, which is computed for N pieces as UB(N) = 40 * 10^(N-2) * C(10,N-2) (40 is the number of king placements):
Pieces NULP Upper bound Upper bound / NULP
2 20 40 2.0000
3 1,746 4,000 2.2910
4 69,556 180,000 2.5878
5 1,635,355 4,800,000 2.9351
6 25,117,392 84,000,000 3.3443
7 264,331,909 1,008,000,000 3.8134
8 1,936,519,455 8,400,000,000 4.3377
9 9,770,507,866 48,000,000,000 4.9127
10 32,535,116,698 180,000,000,000 5.5325
11 64,617,989,055 400,000,000,000 6.1902
12 58,151,957,864 400,000,000,000 6.8785
Looking at the ratios (UB/NULP) you can quickly see they grow quadratically:2.0000 2.2910 2.5878 2.9351 3.3443 3.8134 4.3377 4.9127 5.5325 6.1902 6.8785
0.2910 0.2968 0.3473 0.4092 0.4691 0.5243 0.5750 0.6198 0.6577 0.6883
0.0058 0.0505 0.0619 0.0599 0.0552 0.0507 0.0448 0.0379 0.0306
Therefore we can try to see if 4x4 has the same quadratic growth, and if so, use it to predict the NULP in 4x4. We already know the NULP up to 10 pieces:Pieces NULP
2 21
3 3,378
4 227,863
5 8,800,193
6 226,574,229
7 4,143,017,722
8 56,477,398,248
9 582,113,235,900
10 4,601,321,236,958
Upper bounds in 4x4 can be computed the same simple way: UB(N) = 78 * 10^(N-2) * C(14,N-2) (this time 78 king placements):Pieces Upper bound
2 78
3 10,920
4 709,800
5 28,392,000
6 780,780,000
7 15,615,600,000
8 234,234,000,000
9 2,676,960,000,000
10 23,423,400,000,000
11 156,156,000,000,000
12 780,780,000,000,000
13 2,839,200,000,000,000
14 7,098,000,000,000,000
15 10,920,000,000,000,000
16 7,800,000,000,000,000
So the known UB/NULP ratios in 4x4 are:Pieces Upper bound / NULP
2 3.7143
3 3.2327
4 3.1150
5 3.2263
6 3.4460
7 3.7691
8 4.1474
9 4.5987
10 5.0906
3.7143 3.2327 3.1150 3.2263 3.4460 3.7691 4.1474 4.5987 5.0906
-0.4816 -0.1177 0.1113 0.2197 0.3231 0.3783 0.4513 0.4919
0.3639 0.2290 0.1084 0.1034 0.0552 0.0730 0.0406
When using all numbers from 2 to 10 pieces, quadratic curve fits, but not very well, so I chose to skip the first two numbers, and use only 4-to-10 pieces for extrapolation.
First thing that is apparent is that contraty to my previous simple assumption, the UB/NULP ratio is not the same between 3x4 and 4x4. It is consistently larger in 4x4, even if not much, and the gap is widening when larger part of the board is occupied.
Quadratic curve gives quite decent fit (4 to 10 pieces), so I extrapolated to 16 pieces, getting these ratios:
Pieces Upper bound / NULP
11 5.721838
12 6.399510
13 7.152963
14 7.982198
15 8.887213
16 9.868010
Putting these ratios and the upper bounds together, NULP values are estimated as:Pieces NULP
11 27,291,229,948,942
12 122,006,216,100,920
13 396,926,420,561,661
14 889,228,756,289,934
15 1,228,731,661,995,724
16 790,432,924,166,068
Summing all NULPs from 2 to 16 pieces, we obtain the overall estimated NULP as 3,459,861,499,557,761 = 3.460 peta-positions. Or 3.460 peta-bytes, if uncompressed database is stored with 1 byte for each position. This is smaller than previous estimate of 3.947 peta-positions, and probably close to the true number.The estimated NULP (number of unique legal positions) in 4x4 chess is 20,680 times larger than the actual NULP in 3x4 chess.
EDIT: 2011-01-31: cleanup.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
I discovered that I double-counted some positions. So the 4x4 NULP values I posted above are larger than the correct ones by about 0.2%. I'll post the correct numbers later.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Finally I have a seemingly functional 4x4 chess solver - that is, it can build DTM tables which pass verification. It's very rough bare solver, no compression, no other metrics, no mining, no stats, no web-interface, etc.. It's full of debugging code, and I did not even begin optimizing for speed.
So far I generated up to 7-piece tables, and verified up to 6-piece. Generation of 8-piece tables and verification of 7-piece are ongoing. I'll be posting more details in the coming weeks.
If you'd like to help testing, or to just play with it, let me know.
Can you guess the longest line length with 3 pieces, 4, 5, etc? (Also, which piece configuration has the longest line?)
So far I generated up to 7-piece tables, and verified up to 6-piece. Generation of 8-piece tables and verification of 7-piece are ongoing. I'll be posting more details in the coming weeks.
If you'd like to help testing, or to just play with it, let me know.
Can you guess the longest line length with 3 pieces, 4, 5, etc? (Also, which piece configuration has the longest line?)
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
-
Arpad Rusz
- Posts: 93
- Joined: Mon Mar 27, 2006 5:33 pm
- Sign-up code: 0
- Location: Romania/Hungary
- Contact:
Re: 4x4 chess
3 men pawnless tablebases: the KR/K endgame has the longest line. Maximum DTM probably 8. (Ka1,Rd4/Kc3)Kirill Kryukov wrote:Can you guess the longest line length with 3 pieces, 4, 5, etc? (Also, which piece configuration has the longest line?)
3 men pawnful tablebases: the KP/K endgame has the longest line. (That was easy.
4 men pawnless tablebases: 18 moves? (maybe the KR/KN)
4 men pawnful tablebases: KR/KP?
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Hi Arpad!
 The longest 12 moves is correct though. Good job! (Although with no mining function implemented, I don't know the maxDTM position yet)
The longest 12 moves is correct though. Good job! (Although with no mining function implemented, I don't know the maxDTM position yet)

4-man pawnful - KR/KP is correct!
I'll try to post the positions this weekend. Any more guesses welcome.
EDIT: Correction.
Yeah, of course KRK for pawnless, however maxDTM is only 7 moves. "Ka1,Rd4/Kc3" is one of those mates in 7: "3R/2k1/4/K3 w - - 0 1" 1.Ra4 Kb3 2.Ra2 Kc3 3.Ra3+ Kc2 4.Ka2 Kc1 5.Kb3 Kd2 6.Kb2 Kd1 7.Rd3# (If you find a hole, please tell me!).Arpad Rusz wrote:3 men pawnless tablebases: the KR/K endgame has the longest line. Maximum DTM probably 8. (Ka1,Rd4/Kc3)
Sorry, no WPb4 or Kb8 on 4x4 board please.Arpad Rusz wrote:3 men pawnful tablebases: the KP/K endgame has the longest line. (That was easy.) My guess for longest line is 12. (Kd4,Pb4/Kb8)
4-man pawnless - more than 18 moves, not KR/KN.Arpad Rusz wrote:4 men pawnless tablebases: 18 moves? (maybe the KR/KN)
4 men pawnful tablebases: KR/KP?
4-man pawnful - KR/KP is correct!
I'll try to post the positions this weekend. Any more guesses welcome.
EDIT: Correction.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Status update. 7-piece DTM verified OK, 8-piece DTM computation is underway. 3-to-5-piece DTC and DTZ tables are built and verified with no errors.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
-
Arpad Rusz
- Posts: 93
- Joined: Mon Mar 27, 2006 5:33 pm
- Sign-up code: 0
- Location: Romania/Hungary
- Contact:
Re: 4x4 chess
Correct! I played 5.Rc3 instead of 5.Kb3!.Kirill Kryukov wrote:Yeah, of course KRK for pawnless, however maxDTM is only 7 moves. "Ka1,Rd4/Kc3" is one of those mates in 7: "3R/2k1/4/K3 w - - 0 1" 1.Ra4 Kb3 2.Ra2 Kc3 3.Ra3+ Kc2 4.Ka2 Kc1 5.Kb3 Kd2 6.Kb2 Kd1 7.Rd3# (If you find a hole, please tell me!).
This was my position: (Kd1,Pb1/Kb4 12#). Sorry for the wrong coordinates.Kirill Kryukov wrote:Sorry, no WPb4 or Kb8 on 4x4 board please.The longest 12 moves is correct though. Good job! (Although with no mining function implemented, I don't know the maxDTM position yet)
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Great, yes, this is 12#! According to the database, there are 3 more wins in 12 in kpk. (Unique positions, not just reflections).Arpad Rusz wrote:This was my position: (Kd1,Pb1/Kb4 12#). Sorry for the wrong coordinates.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
-
Arpad Rusz
- Posts: 93
- Joined: Mon Mar 27, 2006 5:33 pm
- Sign-up code: 0
- Location: Romania/Hungary
- Contact:
Re: 4x4 chess
Yes, the wK can be shifted to c1,d2, or d3 and after 1.Kc2 the result is the same as in (Kd1,Pb1/Kb4).Kirill Kryukov wrote:Great, yes, this is 12#! According to the database, there are 3 more wins in 12 in kpk. (Unique positions, not just reflections).Arpad Rusz wrote:This was my position: (Kd1,Pb1/Kb4 12#). Sorry for the wrong coordinates.
So probably these are the other 3 maximum length positions: (Kc1, Pb1/Kb4), (Kd2, Pb1/Kb4) and (Kd3, Pb1/Kb4).
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
(Kc1, Pb1/Kb4) is only mate in 9, throuhg 1.Kb2. The other two are wins in 12. So one more win in 12 is unknown.Arpad Rusz wrote:Yes, the wK can be shifted to c1,d2, or d3 and after 1.Kc2 the result is the same as in (Kd1,Pb1/Kb4).
So probably these are the other 3 maximum length positions: (Kc1, Pb1/Kb4), (Kd2, Pb1/Kb4) and (Kd3, Pb1/Kb4).
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
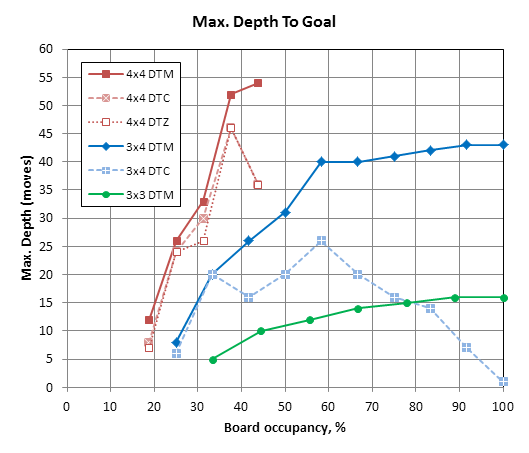
Since there are no more guesses, here is the summary of currently known 4x4 chess MaxDepth values, compared with all known values from 3x4 and 3x3 chess:
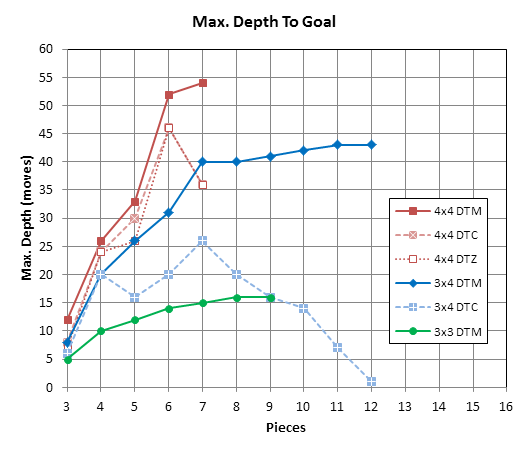
Yes, 52 moves DTM with 6 pieces, 54 with 7 pieces. (I still did not walk through the lines or even saw the maximum positions, so please be careful with this data. Although automatic verification shows no errors).
Some of the questions (other than the ultimate one "what is the overall max. depth in each metric?"):
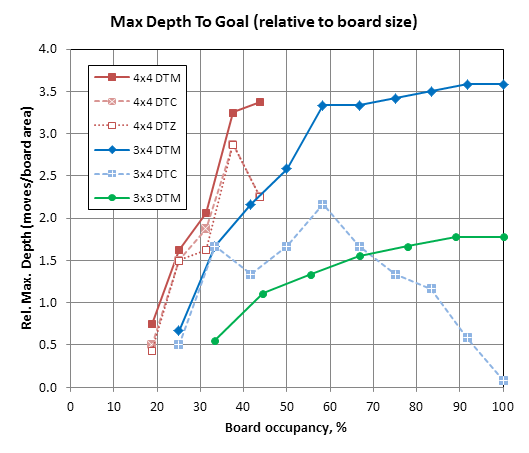
The same graph, after dividing max.depth by board area. Sort of showing how many times each square can be visited by each side during the longest line.

Yes, 52 moves DTM with 6 pieces, 54 with 7 pieces. (I still did not walk through the lines or even saw the maximum positions, so please be careful with this data. Although automatic verification shows no errors).
Some of the questions (other than the ultimate one "what is the overall max. depth in each metric?"):
- Did 4x4 DTM reach the plateau at 6 pieces? (We can see that 3x4 DTM reached plateau at 7 pieces, and grew only slowly since then. It would be surprising if at 4x4 the plateau starts with only 6 pieces.)
- For how long 4x4 DTC and DTZ will remain overlapping?
- Will both 4x4 DTC and DTZ continue to fall after 6 pieces, or will they experience another peak? (3x4 DTC has 2 peaks).

The same graph, after dividing max.depth by board area. Sort of showing how many times each square can be visited by each side during the longest line.

KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Database sizes for 3x4 and 4x4 chess.
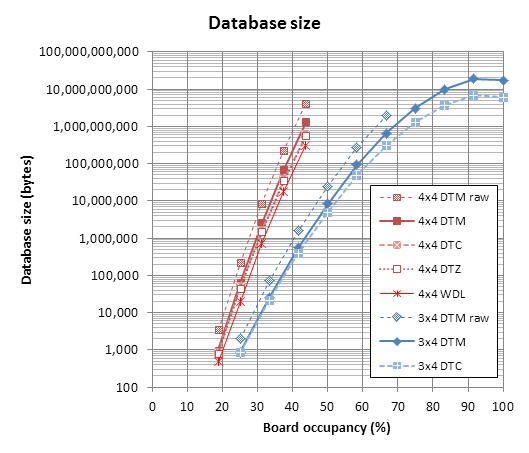
"raw" means uncompressed, the rest are all compressed (2 metrics on 3x4 and 4 metrics on 4x4 board). Board occupancy means how large area of the board is occupied. e.g., 3 pieces on 4x4 board means 3/16 = 18.75% occupancy.
In 3x4 chess the raw (uncompressed) database is up to 8 pieces only. In 4x4 chess the raw database, as well as compressed ones in 4 metrics are compared up to 7 pieces.
Nothing really unexpected here.

"raw" means uncompressed, the rest are all compressed (2 metrics on 3x4 and 4 metrics on 4x4 board). Board occupancy means how large area of the board is occupied. e.g., 3 pieces on 4x4 board means 3/16 = 18.75% occupancy.
In 3x4 chess the raw (uncompressed) database is up to 8 pieces only. In 4x4 chess the raw database, as well as compressed ones in 4 metrics are compared up to 7 pieces.
Nothing really unexpected here.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Compactness of different metrics:
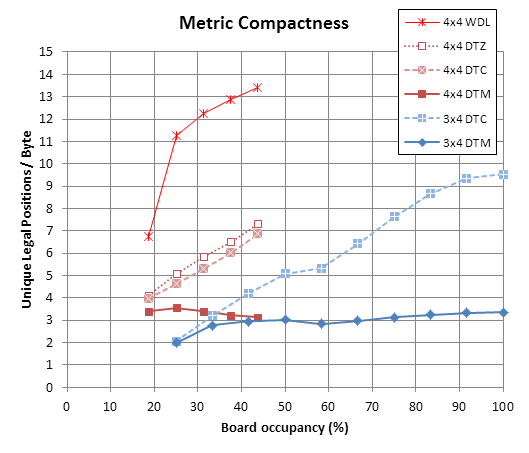
All compressed. 2 metrics in 3x4 (3 to 12 pieces), 4 metrics in 4x4 (3 to 7 pieces).
Some observations:
- DTM is around 3 pos/byte in both 3x4 and 4x4, slightly more compact in 4x4.
- The gap between DTC and DTM is wider on larger board.
- DTZ and DTC are very close to each other, and more or less parallel from 4 pieces.
- WDL is much more compact than the other metrics, but still not as much as I expected (since it's even more compact on larger boards).
Note that DTZ, DTC and WDL will all have to meet each other at 100% occupancy.

All compressed. 2 metrics in 3x4 (3 to 12 pieces), 4 metrics in 4x4 (3 to 7 pieces).
Some observations:
- DTM is around 3 pos/byte in both 3x4 and 4x4, slightly more compact in 4x4.
- The gap between DTC and DTM is wider on larger board.
- DTZ and DTC are very close to each other, and more or less parallel from 4 pieces.
- WDL is much more compact than the other metrics, but still not as much as I expected (since it's even more compact on larger boards).
Note that DTZ, DTC and WDL will all have to meet each other at 100% occupancy.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
I'm testing the 4x4 chess database interface, any help with testing will be appreciated. It's still buggy and lacks features. Some maxDTM positions as examples:
5 pieces, mate in 33
6 pieces, mate in 52
(although any position can be queried by putting a proper FEN into the address line).
Notation explanation and other help pages are still missing and will be added soon (hopefully).
Please let me know if it does not work for you, if it does not display properly, or if you notice anything else strange or broken. Any questions or ideas are welcome as always!
5 pieces, mate in 33
6 pieces, mate in 52
(although any position can be queried by putting a proper FEN into the address line).
Notation explanation and other help pages are still missing and will be added soon (hopefully).
Please let me know if it does not work for you, if it does not display properly, or if you notice anything else strange or broken. Any questions or ideas are welcome as always!
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
-
Arpad Rusz
- Posts: 93
- Joined: Mon Mar 27, 2006 5:33 pm
- Sign-up code: 0
- Location: Romania/Hungary
- Contact:
Re: 4x4 chess
Nice! What are those circles and squares?
Re: 4x4 chess
Forbidden
You don't have permission to access /chess/4x4-chess/ on this server.
3.Nb1+□ ??2rp/k1N1/2R1/K3 w - - 0 1
1.Na4?? Rxc2☉!! 2.Nc3 Rc1+ 3.Nb1+□
Otherwise great work. It was fun walking through the 52# line you provided.
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Sorry, I know it's confusing, I should add the notation legend soon. In the meantime:Arpad Rusz wrote:Nice! What are those circles and squares?
"□" - The only possible move
"♢" - Winning move, which has equally good alternatives.
"☉" - Move leads to a mutual zugzwang.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Thanks for testing!! OK, this one is fine for now, as the "home" page does not exist yet.Codeman wrote:Forbidden
You don't have permission to access /chess/4x4-chess/ on this server.
Looks OK to me? "□" means the only possible move. It should really look like a blank square, so it's not a missing symbol.Codeman wrote:3.Nb1+□ ??2rp/k1N1/2R1/K3 w - - 0 1
1.Na4?? Rxc2☉!! 2.Nc3 Rc1+ 3.Nb1+□
Oh.. Good find, I'll debug and fix this.Codeman wrote:
Right, this is a bug as well (hopefully the same one).Codeman wrote:
This too.Codeman wrote:
Thanks!!Codeman wrote:Otherwise great work. It was fun walking through the 52# line you provided.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
-
Arpad Rusz
- Posts: 93
- Joined: Mon Mar 27, 2006 5:33 pm
- Sign-up code: 0
- Location: Romania/Hungary
- Contact:
Re: 4x4 chess
Then there is a serious bug...Kirill Kryukov wrote:"☉" - Move leads to a mutual zugzwang.
Look at the 5 pieces maxDTM. 1.Rb3 doesn't lead to mutual zugzwang, black just captures the rook.
Probably you have marked with circles the positions with different outcome if WTM and BTM. Only a small percentage of them are really mutual zugzwangs.
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
You are right, of course it's a bug. No, I did not simply mark all positions where WTM and BTM outcomes are different. It was supposed to really mark zugzwangs.Arpad Rusz wrote:Then there is a serious bug...Kirill Kryukov wrote:"☉" - Move leads to a mutual zugzwang.
Look at the 5 pieces maxDTM. 1.Rb3 doesn't lead to mutual zugzwang, black just captures the rook.
Probably you have marked with circles the positions with different outcome if WTM and BTM. Only a small percentage of them are really mutual zugzwangs.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Zugzwang marking should be fixed now. So now there are no zugzwangs in the 5-man MaxDTM line, but there is one in the 6-man maxDTM line, on move 25. 
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP