4x4 chess
4x4 chess
Kirill -
I spent some interesting time looking at your 3x3 chess page, a game you solved a couple years back. Do you know of any 4x4 chess games, and whether they have defined forces and starting positions? There is a gap in the otherwise informative article at en.wikipedia.org/wiki/Minichess, but in his blog, Aloril (the other 3x3 chess solver - who is he?) claims to have built 4x4 tablebases up to size 7.
john
I spent some interesting time looking at your 3x3 chess page, a game you solved a couple years back. Do you know of any 4x4 chess games, and whether they have defined forces and starting positions? There is a gap in the otherwise informative article at en.wikipedia.org/wiki/Minichess, but in his blog, Aloril (the other 3x3 chess solver - who is he?) claims to have built 4x4 tablebases up to size 7.
john
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
There are some 4x4 games on chessvariants web-site. You can find them by opening this page, scrolling down to the query form, entering 4 in "Board Rows:" and "Board Columns:" field and 16 in "Board Cells:" field and pressing "Search".jkominek wrote:Kirill -
I spent some interesting time looking at your 3x3 chess page, a game you solved a couple years back. Do you know of any 4x4 chess games, and whether they have defined forces and starting positions? There is a gap in the otherwise informative article at en.wikipedia.org/wiki/Minichess, but in his blog, Aloril (the other 3x3 chess solver - who is he?) claims to have built 4x4 tablebases up to size 7.
john
By the way I don't think you can create an interesting starting position for 4x4 chess, same like for 3x3. Interesting means the one which allows non-trivial gameplay. Though I think 4x4 chess will contain incredibly interesting longest checkmate lines.
I am interested to solve 4x4 but I don't have time for that at the current moment.
(I don't know much about Aloril. Here is his wiki page, where you can talk to him too.)
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
You are probably right about this, as there'd be no open space between the forces when adopting an analog to the opening of traditional chess. But it does enlarege the problem substantially, as there would be no forward bounding of the search space from the opening position.I don't think you can create an interesting starting position for 4x4 chess, same like for 3x3. Interesting means the one which allows non-trivial gameplay.
To fully solve 4x4 chess, be prepared to evaluate in the range of 283,335,014,381,495 = 283.3 tera positions. This is the size of the Heinz-Wirth index space. Assuming a generous 5:1 compression ratio, it won't compact below 50 TB of final storage. Not to mention the computation and working space required. We have a ways to go yet.
Regarding 3x3 chess, you suggest an interesting issue: that of finding a good game start position, rather than declaring one. This should be a position that can reach a large fraction of the entire space, has equal force on each side, has nearly equal winning chance for white and black, is a game theoritic draw with best play, has multiple draw-preserving moves near the root node for either side (rather than a single best line), but also contains ample complexity to make mistakes common. Plus, it wouldn't hurt if it were amenable to human-like strategic thinking, though that is less an aspect of the starting position than of the game itself.
So maybe you can find something that meets these deserida?
john
[quote="To fully solve 4x4 chess, be prepared to evaluate in the range of 283,335,014,381,495 = 283.3 tera positions. This is the size of the Heinz-Wirth index space. Assuming a generous 5:1 compression ratio, it won't compact below 50 TB of final storage. Not to mention the computation and working space required. We have a ways to go yet."
[/quote]
Hi John,
Is this number for one set of pieces or all ? IMO there are much more positions to be examined. E.g. when I have 16 pieces there are 1 * 2 * 3 .... * 15 * 16 positions ( approx. 21 tera positions ). When you divide this by 8 you still have 2.6 tera positions to examine for one set only.
With 8 v 8 you will surely find several thousand sets.
So I think solving 4x4 chess would be much more difficult.
BTW what do you mean with "Hein-Wirth index space" ?
Lutz
[/quote]
Hi John,
Is this number for one set of pieces or all ? IMO there are much more positions to be examined. E.g. when I have 16 pieces there are 1 * 2 * 3 .... * 15 * 16 positions ( approx. 21 tera positions ). When you divide this by 8 you still have 2.6 tera positions to examine for one set only.
With 8 v 8 you will surely find several thousand sets.
So I think solving 4x4 chess would be much more difficult.
BTW what do you mean with "Hein-Wirth index space" ?
Lutz
Ernest -- Not much. Wikipedia and the Chess Variants website have short articles. I plan to look up the Martin Gardner article in which he introduces the game.
http://en.wikipedia.org/wiki/Minichess
http://www.chessvariants.org/small.dir/hpmini.html
In the Wikipedia article I'm intruiged by the popularity 5x5 chess gained in Italy, especially the development of opening theory. Alas, I could find nothing on the current Associazione Italiana Scacchi Eterodossi website, except old member profile pages stating that they play the game. Perhaps our Italian friends can help out. (guido?)
john
http://en.wikipedia.org/wiki/Minichess
http://www.chessvariants.org/small.dir/hpmini.html
In the Wikipedia article I'm intruiged by the popularity 5x5 chess gained in Italy, especially the development of opening theory. Alas, I could find nothing on the current Associazione Italiana Scacchi Eterodossi website, except old member profile pages stating that they play the game. Perhaps our Italian friends can help out. (guido?)
john
Hi Lutz,
Thanks for you interest. I have revised numbers to present, but first a point of clarification. I'm referring to "index space size" of the entire game, not just one combination. This is different - usually smaller - than the number of physical positions possible on the board.
The simplest index space is Euclidean: 64 squares for regular chess, 13 possibilities per square, for 1.96x10^71 piece occupancies. Double this for side-to-move information, and again for white and black castling rights, and throw in the 50 move counter to support all possible chess positions. In my calculations the only state information I bother with is side-to-move. Serious efforts need to consider en passant.
The above scheme doesn't prohibit multiple pieces from occupying the same square, and so is an overestimate. Computing n! as you did provides a tighter upper bound. But you can go further. The main ones are: symmetry of the chess board (8-way for pawnless, 2-way with pawns), identical piece symmetry (two pieces of the same color can be interchanged, a savings of half), constraints on pawn location (middle 48 of the board), and king restrictions (they can't touch). Further, Nalimov has a complicated mechanism for eliminating some of the "broken" positions.
The "Heinz/Wirth" scheme uses pure combinatorics for computing the index space of a given piece combination, and I've written a program to do that. The Nalimov scheme runs about 8% more compact, but requires an actual chess unmove generator to calculate the result (i.e. you need to run tbgen). The best article I know on the topic is "Space-Efficient Indexing of Chess Endgame Tables" by Nalimov, Haworth, and Heinz; ICGA, Sept. 2000. You can find it at Guy's website.
"Heinz/Wirth" as I call it comes from two chess programmers that worked on endgame constrution during the mid to late 90s (independently, there are slight differences). From what I read, the seminal names in tablebase construction are, in chronologial order:
Ken Thompson (groundbreaker)
Steven Edwards
Lewis Stiller
Ernest Heinz
Christoph Wirth
Eugene Nalimov (most famously)
To which perhaps Konoval, Bourzutschky, and Antonelli will have their names added.
My current numbers for 4x4 chess are smaller than in my previous post. The reason is that I've pruned out impossible force combinations, such as 6 rooks on one side.
Technically, read "TB" etc. not as terabytes but as tera positions, though I doubt max-dtm exceeds 127.
There is a qualifications. I'm restricting pawns to the middle two ranks. This is wrong because 4x4 chess has no defined starting position. But, I wanted to stick with the same code that I use for computing the index space of regular 8x8 chess. I can post a detailed file of the 45150 combinations if you'd like.
john
Thanks for you interest. I have revised numbers to present, but first a point of clarification. I'm referring to "index space size" of the entire game, not just one combination. This is different - usually smaller - than the number of physical positions possible on the board.
The simplest index space is Euclidean: 64 squares for regular chess, 13 possibilities per square, for 1.96x10^71 piece occupancies. Double this for side-to-move information, and again for white and black castling rights, and throw in the 50 move counter to support all possible chess positions. In my calculations the only state information I bother with is side-to-move. Serious efforts need to consider en passant.
The above scheme doesn't prohibit multiple pieces from occupying the same square, and so is an overestimate. Computing n! as you did provides a tighter upper bound. But you can go further. The main ones are: symmetry of the chess board (8-way for pawnless, 2-way with pawns), identical piece symmetry (two pieces of the same color can be interchanged, a savings of half), constraints on pawn location (middle 48 of the board), and king restrictions (they can't touch). Further, Nalimov has a complicated mechanism for eliminating some of the "broken" positions.
The "Heinz/Wirth" scheme uses pure combinatorics for computing the index space of a given piece combination, and I've written a program to do that. The Nalimov scheme runs about 8% more compact, but requires an actual chess unmove generator to calculate the result (i.e. you need to run tbgen). The best article I know on the topic is "Space-Efficient Indexing of Chess Endgame Tables" by Nalimov, Haworth, and Heinz; ICGA, Sept. 2000. You can find it at Guy's website.
"Heinz/Wirth" as I call it comes from two chess programmers that worked on endgame constrution during the mid to late 90s (independently, there are slight differences). From what I read, the seminal names in tablebase construction are, in chronologial order:
Ken Thompson (groundbreaker)
Steven Edwards
Lewis Stiller
Ernest Heinz
Christoph Wirth
Eugene Nalimov (most famously)
To which perhaps Konoval, Bourzutschky, and Antonelli will have their names added.
My current numbers for 4x4 chess are smaller than in my previous post. The reason is that I've pruned out impossible force combinations, such as 6 rooks on one side.
Code: Select all
1. Promotions: all
King Positions w/o pawns: 21
King Positions with pawns: 78
Len: 2 1 21 21.0 B
Len: 3 4 3,012 3.0 kB
Len: 4 20 174,876 0.2 MB
Len: 5 60 5,819,424 5.8 MB
Len: 6 170 127,490,064 0.1 GB
Len: 7 395 1,973,061,792 2.0 GB
Len: 8 857 22,429,944,966 22.4 GB
Len: 9 1656 191,249,920,992 0.2 TB
Len: 10 2892 1,223,581,967,790 1.2 TB
Len: 11 4445 5,764,492,849,752 5.8 TB
Len: 12 6195 19,333,125,836,388 19.3 TB
Len: 13 7665 43,880,342,399,712 43.9 TB
Len: 14 8393 62,036,159,467,464 62.0 TB
Len: 15 7546 46,354,925,477,952 46.4 TB
Len: 16 4851 11,664,066,763,440 11.7 TB
-------------------
Total 45150 190,472,481,177,645 0.2 PBThere is a qualifications. I'm restricting pawns to the middle two ranks. This is wrong because 4x4 chess has no defined starting position. But, I wanted to stick with the same code that I use for computing the index space of regular 8x8 chess. I can post a detailed file of the 45150 combinations if you'd like.
john
Hi John,
Thank you for your clear answer. It would be great if you could either post the detailed list or send it to me by email. I want to create my own program to get more familar with these technics and will check my results against yours.
For now I have onyl two questions:
1. I found 29 valid king positions w/o pawns:
WKa1 BK = a4-d4, a3-d3, c2,d2,c1,d1 = 12
WKa2 BK = a4-d4, c1-c3,d1-d3 = 10
WKb2 BK = a4-d4. d1-d3 = 7
What did I miss?
King poisitons with pawns are 78. That's clear.
2. Aren't there 5 piece combinations for 3-piece endgames (P,N,K,R,Q) ?
Shoudn't the number of combinations be the same as for endgames on a 8x8 board ? ok, there is a max of 5 for Q, R.. but that can be ignored for endgames till 7 pieces.
Lutz
Thank you for your clear answer. It would be great if you could either post the detailed list or send it to me by email. I want to create my own program to get more familar with these technics and will check my results against yours.
For now I have onyl two questions:
1. I found 29 valid king positions w/o pawns:
WKa1 BK = a4-d4, a3-d3, c2,d2,c1,d1 = 12
WKa2 BK = a4-d4, c1-c3,d1-d3 = 10
WKb2 BK = a4-d4. d1-d3 = 7
What did I miss?
King poisitons with pawns are 78. That's clear.
2. Aren't there 5 piece combinations for 3-piece endgames (P,N,K,R,Q) ?
Shoudn't the number of combinations be the same as for endgames on a 8x8 board ? ok, there is a max of 5 for Q, R.. but that can be ignored for endgames till 7 pieces.
Lutz
Hi Lutz,
You missed a diagonal symmetry that e.g. Nalimov incorporates in his indexing scheme.
When the white king is on the a1-d4 diagonaly, the location is the black king is symmetric about this diagonal (one board position can be transformed into the other without changing the dtm value). In these situations the black king is restricted to the a1-d1-d4 triangle.
WK a1, BK != a4,b4,c4,a3,b3 = 5
WK b2, BK != a4,b4,c4 = 3
29-8=21
For you second question -- I'm mimicking regular chess as much as possible. Thus I give each side 4 pawns and 4 pieces, and assume that pawns can promote to non-king pieces. In my case I go with a {k,q,r,b} nomenclature. When there are N=3 men on the board, the 4 combinations are kpk, kbk, krk, kqk. Allowing the knight on the board I get a total of 3,606,864,496,135,089 positions, larger by almost 20.
Attached is a detailed listing of my 4x4 computation (without knights).
john
You missed a diagonal symmetry that e.g. Nalimov incorporates in his indexing scheme.
When the white king is on the a1-d4 diagonaly, the location is the black king is symmetric about this diagonal (one board position can be transformed into the other without changing the dtm value). In these situations the black king is restricted to the a1-d1-d4 triangle.
WK a1, BK != a4,b4,c4,a3,b3 = 5
WK b2, BK != a4,b4,c4 = 3
29-8=21
For you second question -- I'm mimicking regular chess as much as possible. Thus I give each side 4 pawns and 4 pieces, and assume that pawns can promote to non-king pieces. In my case I go with a {k,q,r,b} nomenclature. When there are N=3 men on the board, the 4 combinations are kpk, kbk, krk, kqk. Allowing the knight on the board I get a total of 3,606,864,496,135,089 positions, larger by almost 20.
Attached is a detailed listing of my 4x4 computation (without knights).
john
- Attachments
-
- chess_posn_counts.4x4.details.gz
- (444.35 KiB) Downloaded 994 times
Thanks again for your help and the data. So far it's clear now.
With a normal PC we should be able to calc all endgames up to 9 or 10 pieces.
IMO there are wrong combinations in your file,
e.g. 45144 4846 kqqqqqrrkqqqqqpp 72,648,576 72.6 MB
4 pawns exchanged to a queen so there shouldn't be any further pawns available.
Lutz
With a normal PC we should be able to calc all endgames up to 9 or 10 pieces.
IMO there are wrong combinations in your file,
e.g. 45144 4846 kqqqqqrrkqqqqqpp 72,648,576 72.6 MB
4 pawns exchanged to a queen so there shouldn't be any further pawns available.
Lutz
Lutz --
Yes, I agree you're right! Let me figure out how they got in there and report back with corrected figures. (Already have a good idea of where the mistake lies.)
Thanks for drawing my attention to this. It implies a smaller number of positions, for one thing. Which is good news. Will find out what the exact savings is, but solving 4x4 chess is within reach of a current high-end PC, I believe. Maybe you plan to take a shot at it?
john
Yes, I agree you're right! Let me figure out how they got in there and report back with corrected figures. (Already have a good idea of where the mistake lies.)
Thanks for drawing my attention to this. It implies a smaller number of positions, for one thing. Which is good news. Will find out what the exact savings is, but solving 4x4 chess is within reach of a current high-end PC, I believe. Maybe you plan to take a shot at it?
john
Hi,
Well, I think I've got all board combinations with impossible force pruned out, but I wouldn't mind you double-checking. The new results are attached.
The total number of positions has gone down from 190.5 T to 151.5 T: 20.4% less.
john
Well, I think I've got all board combinations with impossible force pruned out, but I wouldn't mind you double-checking. The new results are attached.
The total number of positions has gone down from 190.5 T to 151.5 T: 20.4% less.
john
- Attachments
-
- chess_posn_counts.4x4.lst.gz
- (244.57 KiB) Downloaded 941 times
Hi John,
Thank you for the second list. It looks good now.
Yes, I will try to solve 4x4 chess. The files are small enough to get some quick results.
First of all I want to check how I can improve the index scheme, also to learn more about it. Second I have some ideas to store the results with a better compression method. It will shurly take some years but maybe we can work together and spread the results over the net till harddisks become big enough.
I will first start to calculate the number of valid positions for every combination to get a lower bound.
Lutz
Thank you for the second list. It looks good now.
Yes, I will try to solve 4x4 chess. The files are small enough to get some quick results.
First of all I want to check how I can improve the index scheme, also to learn more about it. Second I have some ideas to store the results with a better compression method. It will shurly take some years but maybe we can work together and spread the results over the net till harddisks become big enough.
I will first start to calculate the number of valid positions for every combination to get a lower bound.
Lutz
Re: 4x4 chess
Hi,
There is a 4x4 chess board used in many schools for introducing chess called Tic Tac Chec. The rules are interesting as play starts on an empty board and pieces are placed anywhere on the board as a turn. After the first 3 pcs are placed they can be moved and capture as in regular chess, however captured pieces are returned and can be played again on any unoccupied square as a turn. The object is just to get 4 pcs in a row. Only 1 rook, 1 bishop, 1 knight and 1 pawn per player. The pawn can reverse direction as it's promotion on reaching the opposite side of the board.
So what is the number of possibilities involved and can a computer be optimized to win in as few moves as possible?
Cheers
There is a 4x4 chess board used in many schools for introducing chess called Tic Tac Chec. The rules are interesting as play starts on an empty board and pieces are placed anywhere on the board as a turn. After the first 3 pcs are placed they can be moved and capture as in regular chess, however captured pieces are returned and can be played again on any unoccupied square as a turn. The object is just to get 4 pcs in a row. Only 1 rook, 1 bishop, 1 knight and 1 pawn per player. The pawn can reverse direction as it's promotion on reaching the opposite side of the board.
So what is the number of possibilities involved and can a computer be optimized to win in as few moves as possible?
Cheers
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Relatively trivial to solve, unfortunately it seems it did not generate enough interest for someone to actually do it. In fact this game resembles shogi more than chess. I may look into it after I'll resume my computer shogi experiments (which won't be very soon).Flyboy wrote:Hi,
There is a 4x4 chess board used in many schools for introducing chess called Tic Tac Chec. The rules are interesting as play starts on an empty board and pieces are placed anywhere on the board as a turn. After the first 3 pcs are placed they can be moved and capture as in regular chess, however captured pieces are returned and can be played again on any unoccupied square as a turn. The object is just to get 4 pcs in a row. Only 1 rook, 1 bishop, 1 knight and 1 pawn per player. The pawn can reverse direction as it's promotion on reaching the opposite side of the board.
So what is the number of possibilities involved and can a computer be optimized to win in as few moves as possible?
Cheers
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
(Well, the real reason to resurrect this thread is not Tic Tac Chess).
I am curious if anyone did anything regarding 4x4 since the last discussion more than 3 years ago?
Now, that 3x4 verification is complete, I am beginning to think about 4x4 (naturally). I am doing some preliminary calculations (like counting positions and computing memory requirements). I won't trust my numbers until I'll have a verifier, but still it could be fun to exchange some data.
Perhaps joined efforts towards solving 4x4 can succeed sooner, if anyone is still interested.
I am curious if anyone did anything regarding 4x4 since the last discussion more than 3 years ago?
Now, that 3x4 verification is complete, I am beginning to think about 4x4 (naturally). I am doing some preliminary calculations (like counting positions and computing memory requirements). I won't trust my numbers until I'll have a verifier, but still it could be fun to exchange some data.
Perhaps joined efforts towards solving 4x4 can succeed sooner, if anyone is still interested.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re:
My estimates for the number of positions are much larger, probably because I allow pawns on the first rank. I feel that restricting pawns to just two middle ranks would take away too much from the potential complexity and beauty of this variant.jkominek wrote:To fully solve 4x4 chess, be prepared to evaluate in the range of 283,335,014,381,495 = 283.3 tera positions. This is the size of the Heinz-Wirth index space. Assuming a generous 5:1 compression ratio, it won't compact below 50 TB of final storage. Not to mention the computation and working space required. We have a ways to go yet.
OK, first the simplest possible estimate, using 3x4 as reference. The naive upper bound for 3x4 would be 13^12 = 23.3 tera-positions. We now know that the actual number of unique legal positions (NULP) in 3x4 is 167,303,246,916, thus giving a ratio of 139.257. Applying the same ratio to 4x4 we would have 13^16 / 139.257 = 4.778 peta-positions as a very crude estimate.
Adding king placements we can get a much better upper bound. For 3x4: 40 * 11^10 = 1.037 tera-positions. Just 6.201 times larger than the NULP. So, in 4x4 we get 78 * 11^14 / 6.201 = 4.777 peta-positions. Same with the previous one, curiously.
The next step would be to consider that pawns can't be located on the last rank. In 3x4 this means 40 * 11^6 * 10^4 = 708.6 giga-positions = 4.236 times NULP. Thus, in 4x4 we should have 78 * 11^8 * 10^6 / 4.236 = 3.947 peta-positions. This is probably a not too bad estimate already.
Further improvements may be provided by estimating progressively number of positions with each fixed number of pieces. More on this later.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
One way to think about the complexity of 4x4 chess is to look at the number of piece configurations. It's the same with the number of files, needed to store the complete database (assuming each table is stored as a single file).
(Some people like to store black-to-move and white-to-move variants of the same table, for example kqk.w and kqk.b. I prefer to store every table as white-to-move, so I'll have kqk and kkq. This way looks more general to me. The resulting number of files is the same.)
Also I presume that with current 64-bit systems we don't have to split larger-than-2-GB files into chunks anymore (like in case of Nalimov's tables).
Here is are the numbers for complete solution (counting kqk and kkq as separate configurations). No configuration is considered "impossible", so all are counted.
So, almost 2 million files will be written to store the entire 4x4 solution.
Of course it's possible (easy) to join multiple files together, so the actual number of files may be different. (Although I prefer to really keep them as separate files).
Also, if you don't store the kk table, it will be just 1,961,255 files.
(Some people like to store black-to-move and white-to-move variants of the same table, for example kqk.w and kqk.b. I prefer to store every table as white-to-move, so I'll have kqk and kkq. This way looks more general to me. The resulting number of files is the same.)
Also I presume that with current 64-bit systems we don't have to split larger-than-2-GB files into chunks anymore (like in case of Nalimov's tables).
Here is are the numbers for complete solution (counting kqk and kkq as separate configurations). No configuration is considered "impossible", so all are counted.
Code: Select all
Men Configurations Cumulative
2 1 1
3 10 (x10 ) 11 (x11 )
4 55 (x 5.5 ) 66 (x 6 )
5 220 (x 4 ) 286 (x 4.333)
6 715 (x 3.25 ) 1,001 (x 3.5 )
7 2,002 (x 2.8 ) 3,003 (x 3 )
8 5,005 (x 2.5 ) 8,008 (x 2.667)
9 11,440 (x 2.286) 19,448 (x 2.429)
10 24,310 (x 2.125) 43,758 (x 2.25 )
11 48,620 (x 2 ) 92,378 (x 2.111)
12 92,378 (x 1.9 ) 184,756 (x 2 )
13 167,960 (x 1.818) 352,716 (x 1.909)
14 293,930 (x 1.75 ) 646,646 (x 1.833)
15 497,420 (x 1.692) 1,144,066 (x 1.769)
16 817,190 (x 1.643) 1,961,256 (x 1.714)Of course it's possible (easy) to join multiple files together, so the actual number of files may be different. (Although I prefer to really keep them as separate files).
Also, if you don't store the kk table, it will be just 1,961,255 files.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Facing a huge problem (like solving a game with ~4 quadrillions of unique legal positions) one naturally starts to think about what should be done first, and what can follow later (if at all). Some tables can be computed first, some later, and the exact order is not fixed. Possible orderings follow from the chess rules, however different solving strategies can be designed by giving different orderings different priorities.
Possible orderings may include:
a) all with 3 pieces -> all with 4 pieces -> ... -> all with 16 pieces
b) pawnless endings -> all with 1 pawn -> all with 2 pawns -> ... -> all with 14 pawns
c) pawns only on the middle two ranks -> pawns also on the first rank
d) up to 2 pieces per side -> up to 3 pieces per side -> ... -> up to 15 pieces per side
e) only "possible" piece configurations -> any piece configurations, including "impossible".
Using a particular combination of priorities over these orderings, you can create your preferred path to the complete solution.
It's important to choose a good path, because there is no guarantee that you'll be able to solve everything. So the question is which of the possible incomplete solutions you prefer.
Here I just want to show the effect of (d) ordering (max. number of pieces per side) on the number of piece configurations. In the table below each column corresponds to the different maximum number of pieces per side (M), from 1 to 15 (in reverse order). Each row corresponds to particular total number of pieces, from 2 to 16.
So, for example, if someone thinks that 4x4 chess should not have more than 8 pieces per side, he just needs to generate 627,264 tables, instead of 1,961,256.
I am still undecided whith path to follow, using (a) as a top-level ordering as usual, or (d). I am not interested in (b), (c) or (e) as top level orderings (although of course they are still used as needed at the lower levels).
I'm implementing the possibility to choose between (a), (b) and (d) as the top-level ordering in my solver. I probably won't implement (c) and (e).
Possible orderings may include:
a) all with 3 pieces -> all with 4 pieces -> ... -> all with 16 pieces
b) pawnless endings -> all with 1 pawn -> all with 2 pawns -> ... -> all with 14 pawns
c) pawns only on the middle two ranks -> pawns also on the first rank
d) up to 2 pieces per side -> up to 3 pieces per side -> ... -> up to 15 pieces per side
e) only "possible" piece configurations -> any piece configurations, including "impossible".
Using a particular combination of priorities over these orderings, you can create your preferred path to the complete solution.
It's important to choose a good path, because there is no guarantee that you'll be able to solve everything. So the question is which of the possible incomplete solutions you prefer.
Here I just want to show the effect of (d) ordering (max. number of pieces per side) on the number of piece configurations. In the table below each column corresponds to the different maximum number of pieces per side (M), from 1 to 15 (in reverse order). Each row corresponds to particular total number of pieces, from 2 to 16.
Code: Select all
\ M = 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
Men
2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3 10 10 10 10 10 10 10 10 10 10 10 10 10 10 0
4 55 55 55 55 55 55 55 55 55 55 55 55 55 25 0
5 220 220 220 220 220 220 220 220 220 220 220 220 150 0 0
6 715 715 715 715 715 715 715 715 715 715 715 575 225 0 0
7 2,002 2,002 2,002 2,002 2,002 2,002 2,002 2,002 2,002 2,002 1,750 1,050 0 0 0
8 5,005 5,005 5,005 5,005 5,005 5,005 5,005 5,005 5,005 4,585 3,325 1,225 0 0 0
9 11,440 11,440 11,440 11,440 11,440 11,440 11,440 11,440 10,780 8,680 4,900 0 0 0 0
10 24,310 24,310 24,310 24,310 24,310 24,310 24,310 23,320 20,020 13,720 4,900 0 0 0 0
11 48,620 48,620 48,620 48,620 48,620 48,620 47,190 42,240 32,340 17,640 0 0 0 0 0
12 92,378 92,378 92,378 92,378 92,378 90,376 83,226 68,376 45,276 15,876 0 0 0 0 0
13 167,960 167,960 167,960 167,960 165,230 155,220 133,770 99,120 52,920 0 0 0 0 0 0
14 293,930 293,930 293,930 290,290 276,640 246,610 196,560 127,260 44,100 0 0 0 0 0 0
15 497,420 497,420 492,660 474,460 433,510 363,440 263,340 138,600 0 0 0 0 0 0 0
16 817,190 811,070 787,270 732,670 637,120 496,980 316,800 108,900 0 0 0 0 0 0 0
All 1,961,256 1,955,136 1,926,576 1,850,136 1,697,256 1,445,004 1,084,644 627,264 213,444 63,504 15,876 3,136 441 36 1I am still undecided whith path to follow, using (a) as a top-level ordering as usual, or (d). I am not interested in (b), (c) or (e) as top level orderings (although of course they are still used as needed at the lower levels).
I'm implementing the possibility to choose between (a), (b) and (d) as the top-level ordering in my solver. I probably won't implement (c) and (e).
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Some numbers from test runs: index space, and number of unique legal positions, up to 9 pieces.
I am not confident in these numbers, because I am still testing the data structures, slice iterator, etc., and there is no verifier yet.
One good thing is that index efficiency is not too bad. It's decreasing quickly when adding the first few pieces, but the decrease is slowing down around 8 and 9 pieces. So hopefully the efficiency may be above 75% for the complete database.
Code: Select all
Men Index space Unique legal
2 21 21 (100.00%)
3 3,450 3,378 ( 97.91%)
4 238,725 227,863 ( 95.45%)
5 9,672,330 8,800,193 ( 90.98%)
6 260,262,033 226,574,229 ( 87.06%)
7 4,922,010,421 4,143,017,722 ( 84.17%)
8 68,522,731,579 56,477,398,248 ( 82.42%)
9 712,347,434,276 582,113,235,900 ( 81.72%)One good thing is that index efficiency is not too bad. It's decreasing quickly when adding the first few pieces, but the decrease is slowing down around 8 and 9 pieces. So hopefully the efficiency may be above 75% for the complete database.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
Number of checkmates, among the unique legal positions:
(The first test numbers, without any verification).
Basically the percentage of checkmates seems to be following the same slope like in 3x4 chess:
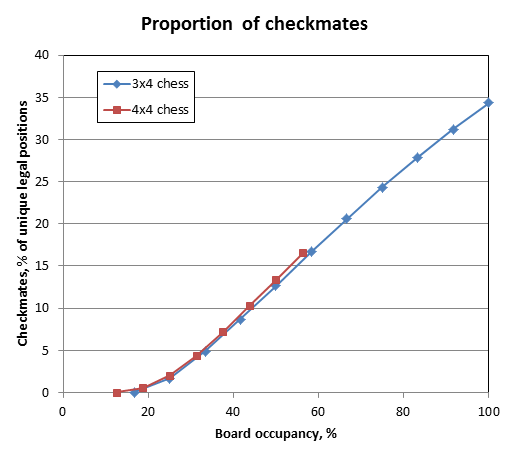
Code: Select all
Men Checkmates
2 0 ( 0.00%)
3 19 ( 0.56%)
4 4,568 ( 2.00%)
5 383,229 ( 4.35%)
6 16,253,172 ( 7.17%)
7 424,524,531 (10.25%)
8 7,555,997,416 (13.38%)
9 96,380,621,318 (16.56%)Basically the percentage of checkmates seems to be following the same slope like in 3x4 chess:

KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
I think I found a good analogy to summarize the difference between 3x4 and 4x4 chess. 3x4 could be (and was) solved in "Alpine" style - a relatively quick and direct effort (even if it took some time, the process was straightforward). In contrast, 4x4 clearly is an "expedition" style project, at least for me. Careful and long siege is ahead, with lot of preparation before the final push. Right now I am not even at the base camp, perhaps just planning and testing the gear. Of course a single-man expedition is unheard of so additional members are very welcome to join (if you're good). For now I am just hoping I'll have enough energy to solve some sizeable part of it before I run out of supplies.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
Re: 4x4 chess
Instead of limiting the number of pieces, you could limit the number of piece types.
Doing up to 4 piece types should be doable now but the full set is about 2^16 times bigger. (actually less as this does not consider that pawns can't be on final rank).
Compression seems very unlikely to buy you very much, so I think you need to get hold of lots of disks to do the full set, or wait some time longer.
If you write software to handle a reduced set of piece types it should be easy to expand as hardware becomes available.
(At least if you write it with that in mind.)
Doing up to 4 piece types should be doable now but the full set is about 2^16 times bigger. (actually less as this does not consider that pawns can't be on final rank).
Compression seems very unlikely to buy you very much, so I think you need to get hold of lots of disks to do the full set, or wait some time longer.
If you write software to handle a reduced set of piece types it should be easy to expand as hardware becomes available.
(At least if you write it with that in mind.)
- Kirill Kryukov
- Site Admin
- Posts: 7399
- Joined: Sun Dec 18, 2005 9:58 am
- Sign-up code: 0
- Location: Mishima, Japan
- Contact:
Re: 4x4 chess
You mean, something like John did above by leaving out the knights? Yes, another possible way. However this is a way to simplify the game, not to optimize the path to the solution of the same game. Because when a piece is left out, the promotions to that piece are not considered, so any tables with pawns will be different from the same table with the full set of pieces. So you can't just fill in the missing tables later, but will have to recompute everything for the complete set of pieces. But yeah, why not. A simpler variant, like 4x4 chess without knights and bishops, should be still interesting.
KCEC | EGTB Online | 3x3 Chess | 3x4 Chess | 4x4 Chess | Longest Checkmates | EGTB Test Suite | Opening Sampler | EGTB Bounty | NULP
Re: 4x4 chess
This is why I am quite interested by the "simpler" variant of 5x5 chess ("italian chess"):Kirill Kryukov wrote:A simpler variant, like 4x4 chess without knights and bishops, should be still interesting.
kqbnr/ppppp/5/PPPPP/KQBNR
Any news about that?